２進数の足し算・引き算（加減算）の方法と正の数・負の数、補数について解説！

１０進数で足し算・引き算（加算・減算）ができるように、２進数でも足し算・引き算ができます。

この記事を読むことで、

・２進数の足し算・引き算（加減算）

・負の数（－）の表し方

・１の補数と２の補数

以上のことが分かります。

また、基数・進数・桁の重みについてより詳しく知りたい方は、

基数とは？IT系国家試験の基本知識、２進数について解説

をご一読ください。基数についてより知ることができます！

２進数の足し算・引き算（加算・減算）

２進数の足し算・引き算は、１０進数の計算と考え方は変わりません。

方法としては、

①２進数を１０進数に変換し、１０進数で計算して出た結果を２進数に再変換する

②２進数のまま計算をする

以上の２つがあります。

２進数の足し算（加算）

①２進数を１０進数に変換し、１０進数で計算して出た結果を２進数に再変換する

メリットは、いつも通りの計算ができる、ということです。

このやり方であれば、いつも通りの計算（１０進数での計算）になるため、１が０が…などと考えなくてすみます。

デメリットは、変換する手間が増え、結果が出るまでに時間がかかる、ということです。

１．１０進数への変換

２．結果を２進数へ再変換

この変換・再変換は大変手間です。

試験などの場合はおすすめのやり方ではありません。

②２進数のまま計算をする

２進数の足し算では、

・０＋０＝０

・１＋０＝１（０＋１＝１）

・１＋１＝１０

以上の３種類で計算ができます。

２進数では「０と１」しか表現できない基数のため、１＋１は桁上がりがおきるのです。

試験などの場合、２進数のまま足し算する方法がおすすめです。

２進数の引き算（減算）

２進数の引き算では、

・０－０＝０

・１－１＝０

・１－０＝１

・０－１＝１

以上の４種類で計算ができます。

０－１＝１の計算に関しては、０から１が引けないため、上の桁から“１”を借りてきます。

１０進数でも、引き算元の数値が足りない場合は、上の桁から数字を借りてきますよね、それと同じです。

１０進数の場合、上から借りてくるものは“１０”になります。

２進数の場合も同じく、上から借りてくるものは“１０”（１０進数に置き換えると“２”）です。

引き算元の数値が足りない場合、上の桁から借りてきます。

・２進数　→　１０（１０進数では“２”）

・10進数　→　１０

負の数（－：マイナス）の表し方

前項では、足し算と引き算の計算のやり方が分かりました。

しかし、これは正の数（＋：プラス）の計算にしか使えません。。

数値は正の数だけではなく、負の数（－：マイナス）が存在します。

負の数の計算はどうすればできるでしょうか？

２進数の考え方で、「先頭の桁（先頭ビット）を符号とする」があります。

例えば、８ビット（１バイト）で数値を表すとします。

その場合、先頭の桁（８桁目）を符号として、０→正の数・１→負の数、とします。

２進数においては、先頭の１ビットを符号用にすることで、正の数・負の数を表すことができるのです。

しかし、上記の数値を計算してみると、

２進数
　０００００１１０＋１００００１１０＝１０００１１００

１０進数
　６＋（‐６）＝０

このように、１０進数ではきちんと解が“０”になりますが、２進数では解が“０”になりません。

この２進数の計算式を成立させるためには、計算結果が“０”になるように負の数を表現する必要があります。そこで登場するのが「補数」です。２進数ではマイナス値の計算を実現するために、「補数」でマイナス値を表現します。

補数とは？

補数とは、補う数という意味です。

補数には以下の２つがあります。

・その桁で最大値になるために補う数

・次の桁に繰り上がるために必要になる補う数

まず、１０進数「５２８」を例に上げて解説します。

・その桁で最大値になるために補う数（９の補数）

５２８は３桁の数値です。

３桁の数値で表せる最大値は「９９９」です。

９９９にするためには、

ｘ＋５２８＝９９９

ｘ＝９９９－５２８

ｘ＝４７１

５２８を９９９にするには、「４７１」を足します。

つまり、４７１という数値を補えば、９９９になる、ということです。

これを「９の補数」と呼びます。

・次の桁に繰り上がるために必要になる補う数（１０の補数）

５２８は３桁の数値です。

３桁の次の桁は４桁なので、繰り上がったすぐの数値は「１０００」です。

１０００にするためには、

ｘ＋５２８＝１０００

ｘ＝１０００－５２８

ｘ＝４７２

５２８を１０００にするには、「４７２」を足します。

つまり、４７２という数値を補えば、１０００になる、ということです。

これを「１０の補数」と呼びます。

・その桁で最大値になるために補う数（１の補数）

それでは、２進数「０１１０」で補数がどうなるかを見てみましょう。

０１１０は４桁の数値です。

４桁の数値で表せる最大値は「１１１１」です。

１１１１にするためには、

ｘ＋０１１０＝１１１１

ｘ＝１１１１－０１１０

ｘ＝１００１

０１１０を１１１１にするには、「１００１」を足します。

つまり、１００１という数値を補えば、１１１１になる、ということです。

これを「１の補数」と呼びます。

１の補数は上記のような計算から求めることもできますが、もっと簡単に補数が分かる方法があります。

元の数値を反転させる、と言う方法です。

０１１０ → １００１ 　①元の数値を反転させる

＝１００１　　　　　　 ②１の補数

反転させることで、１の補数が得られました。

・次の桁に繰り上がるために必要になる補う数（２の補数）

０１１０は４桁の数値です。

４桁の次の桁は５桁なので、繰り上がったすぐの数値は「１００００」です。

１００００にするためには、

ｘ＋０１１０＝１００００

ｘ＝１００００－０１１０

ｘ＝１０１０

０１１０を１００００にするには、「１０１０」を足します。

つまり、１０１０という数値を補えば、１００００になる、と言うことです。

これを「２の補数」と呼びます。

２の補数は上記のような計算から求めることもできますが、もっと簡単に補数が分かる方法があります。

元の数値を反転させ、＋１をする、と言う方法です。

０１１０ → １００１ 　①元の数値を反転させる

１００１＋１　　　　　 ②反転させた数値に＋１をする

＝１０１０          　③２の補数

反転させ＋１で、２の補数が得られました。

２の補数を使った計算

コンピュータにおいて、引き算の計算というものはできません。

そこで、コンピュータでは「２の補数」を使って引き算と同じことを行っているのです。

ここで、前項での計算を補数を使ってやってみましょう。

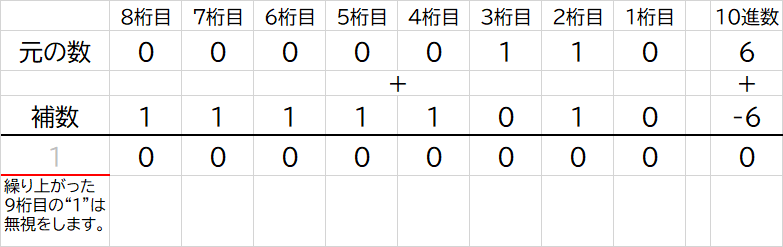
８ビットでの計算をしているため、８ビットから繰り上がりで９ビット目にある“１”は無視をします。

２進数
　０００００１１０＋１１１１１０１０＝００００００００

２進数でも補数を使うことで、正確な計算ができました。

実際に計算をしてみます。

０１１０－００１１

　　　　＋（－００１１）

　　　　１００００－００１１＝１１０１（２の補数）…反転させ、＋１

０１１０＋１１０１＝１００１１
		　　桁上がりした数は無視をする

＝００１１

引き算の計算ができました。

２進数の引き算は、このように「補数」を使うことで計算ができることがわかりました。

まとめ

２進数の足し算・引き算について、分かったでしょうか？

２進数の計算には補数が大変重要になってきます。

理解するには、いくつか計算問題を解いてみていくのが良いでしょう！