２進数の掛け算・割り算（乗除算）の方法とシフト演算（論理シフトと算術シフト）について

１０進数で掛け算・割り算ができるように、他の基数での掛け算・割り算も可能です。

この記事を読むことで、

・２進数の掛け算・割り算（乗除算）

・論理シフト

・算術シフト

以上のことが分かります。

また、基数・進数・桁の重みについてより詳しく知りたい方は、

基数とは？IT系国家試験の基本知識、２進数について解説！

をご一読ください。基数についてより知ることができます！

論理シフトと算術シフト

２進数の掛け算と割り算は、ビットを右や左にずらして行います。

このビットをずらす（シフトする）操作を「シフト演算」と呼びます。

また、このシフト演算には「論理シフト」と「算術シフト」という２つの手法があります。

論理シフト

論理シフトとは、符号を考慮せずにシフトを操作することをいいます。

つまり、先頭ビットも数値として考えてシフトをする、ということです。

２進数の掛け算（乗算）

元の数値を左にシフトすることで、掛け算（２のn乗）ができます。

空いた桁には“０”を入れます。

２進数「１０１０」（１０進数「１０」）を左に１シフト(左論理シフト)することで、

２進数「１０１００」（１０進数「２０」）になり２倍にできました。

また、左論理シフトではあふれたビットは捨てます。

例えば、上記の例が４ビットまでを表すことができるとします。

上記の例では「１０１０」を２倍にしたため、５桁目に数値が入ります。

この場合、４ビットまでしか表せない、となっているため、

５桁目は

「オーバーフロー(桁あふれ)」：扱える範囲の数値の最大値を超えてしまったこと

となり、正確に数値が表せなくなってしまいます。

４ビットまでしか入らないところに５ビットの数値を入れようとしたため起こってしまい、正しい結果を得られません。

（コンピュータで数値を表す場合は、８ビットや１６ビットなどの範囲が多いです）

表現できるビット数には注意しながら計算をするようにしましょう。

２進数の割り算（除算）

元の数値を右にシフトすることで、割り算（ 1/2のn乗）ができます。

“０”があふれた場合は、消します。

２進数「１０１０」（１０進数「１０」）を右に１シフトすることで、

２進数「１０１」（１０進数「５」）になり１／２倍（半分）にできました。

論理シフトでは、符号を考慮せずに計算するため、上記の例のように４桁すべてをシフトして、倍や１／２にすることができました。

また、あふれた数値が"1"だった場合は、割り算の余りとなります。

算術シフト

算術シフトは、論理シフトに符号（＋,－）が付いたものになります。

２進数では、先頭ビットが符号になります。

つまり、先頭ビットは固定して、それ以下の数値のみをシフトをする、ということです。

※２進数の先頭ビットを符号とする場合、０→正・１→負とします。

２進数の符号については、

２進数の足し算・引き算（加減算）の方法と正の数・負の数、補数について解説！　負の数（－：マイナス）の表し方

に詳しく解説してあります。

２進数の掛け算（乗算）

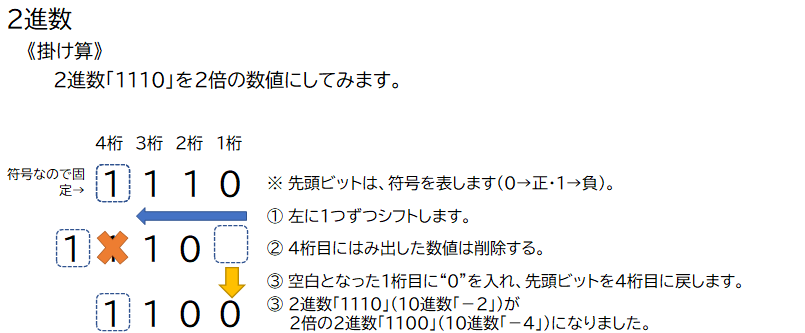
論理シフトと同じく、元の数値を左にシフトすることで、掛け算（２のn乗）ができます。

先頭ビット（４桁目）は符号として扱うため、固定です。

左にシフトし、空いた１桁目には“０”を入れます。

２進数「１１１０」（１０進数「－２」）を左に１シフトすることで、

２進数「１１００」（１０進数「－４」）になり２倍にできました。

また、シフトすることによってあふれたビットが「固定した符号ビットと異なる数値」だった場合は、

論理シフトで説明した「オーバーフロー」が発生してしまいます。

オーバーフローをしたことにより、正しい結果が得られませんでした。

表現できるビット数には注意しながら計算をするようにしましょう。

負の数は元の数値を反転させ、＋１させます。

２進数の割り算（除算）

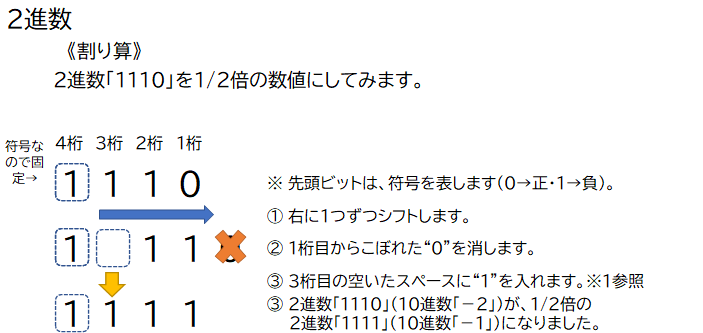
元の数値を右にシフトすることで、割り算（ 1/2のn乗）ができます。

“０”があふれた場合は、消します。

２進数「１１１０」（１０進数「－２」）を右に１シフトすることで、

２進数「１１１１」（１０進数「－１」）になり１／２倍（半分）にできました。

また、あふれた数値が"1"だった場合は、割り算の余りとなります。

図※１

右に算術シフト（算術シフトの割り算）をした場合、空いた桁に入れる数値は先頭ビットによって変わります。

算術シフトの割り算（右シフト）の場合は、空いた桁に入れる数値には注意が必要です！

シフト演算以外の掛け算・割り算

上記までは、右シフトや左シフトをすることで掛け算・割り算の方法を紹介しました。

しかし、シフト演算では

右シフト（掛け算）することで「２・４・８…倍」

左シフト（割り算）することで「１/２・１/４・１/８…倍」

と倍々の計算しかできません。

例えば「３倍」や「５倍」などシフト演算ではできない計算はどうすればよいのでしょうか？

答えは、

掛け算をしたい場合「倍にしたい数値を２の n乗に置き換え、足し算をする」

割り算をしたい場合「元の数値から割りたい数値が２の n乗回、引けるかを計算する」

です。

掛け算

元の数値を５倍にする例（算術シフト）で解説します。

２進数「１１１１１１１０」（１０進数「－２」）が５倍の

２進数「１１１１０１１０」（１０進数「－１０」）になりました。

掛け算をしたい場合

「倍にしたい数値を２の n乗に置き換え、足し算をする」

　倍にしたい数値　　→５

　２の n乗に置き換え→２²と２⁰（４と１）

　足し算をする　　　→（ a × ２²）＋（ b × ２⁰）

ということです。

割り算

今度は、元の数値を１/５倍にする例（論理シフト）で解説します。

２進数「１１０」は１０進数「６」です。

２進数「０００１１１１０」（１０進数「３０」）が１/５倍（÷５）の

２進数「１１０」（１０進数「６」）になりました。

いくつ左にシフトしたかを考えていくと

２²（２ビットシフト）＋２¹（１ビットシフト）

＝４＋２

＝６(０１１０）

元の数値から引くことができた回数は、いくつ２の n乗シフトしたかを足すことで分かります。

また、10進数で考えると、

① ３０－５＝２５

② ２５－５＝２０

③ ２０－５＝１５

④ １５－５＝１０

⑤ １０－５＝５

⑥ ５－５＝０												

３０は５を６回引くことができる、ということです。

このことからも、割り算は引き算で元の数値から何回引けるか、で答えが分かるということです。

割り算をしたい場合

「元の数値から割りたい数値が２の n乗回、引けるかを計算する」		

　元の数値　　　→３０

　割りたい数値　→５

　２の n乗回　　→２²＋２¹

　引けるかを計算→２²＋２¹＝６

ということです。

まとめ

２進数の掛け算・割り算について、シフト演算での方法が分かったでしょうか？

左シフトで掛け算、右シフトで割り算ができます。

また、空いた桁のスペースには“０”を

算術シフトの右シフトの場合にのみ、符号が“１”であれば空いた桁に“１”を入れます。

これは、忘れやすいので注意しましょう。