【超入門IT講座】現代社会に必須！データベースのキホン①
どうもみなさんこんにちは、IT修行中のななこです！ここでは、IT超初心者の私が知りたい！と思ったことにスポットを当て、「なるほど！」と感じたことをご紹介します！今回はITエンジニアになるなら知っておくべき「データベース」の基本について学んだことをお話しますね✨1. データベースとは？データベースは、アプリケーションのデータを保存・蓄積するための手段です！大量のデータを蓄積しておいて、そこから必要な
浮動小数点数の誤差について（無限小数・桁あふれ誤差・情報落ち・打切り誤差・桁落ち・丸め誤差）
Workteria(ワークテリア)では難易度の高いものから低いものまで、スキルや経験に合わせた案件を多数揃えています。会員登録は無料ですので、ぜひ会員登録してご希望の案件を探してみてください！
フリーランス／正社員のエンジニアとして活躍するには、ご自身のスキルや経験に合わせた仕事を選ぶことが大切です。ご希望の案件がみつからない場合はお気軽にお問い合わせください！ユーザ満足度の高いキャリアコンサルタントが在籍していますので、希望条件や悩み事などなんでもご相談ください。ご希望にピッタリの案件をご紹介させていただきます。
２進数を浮動小数点数で表現する際、決まっているビットに入りきらない数が出て、誤差が生じることがありえます。
この記事を読むことで、
・浮動小数点数の誤差
・桁あふれ誤差
・情報落ち
・打ち切り誤差
・丸め誤算
・桁落ち以上のことが分かります。
この記事では、浮動小数点数を知っている方に向けたものとなっています。
浮動小数点数について詳しく知りたい方は、
２進数の小数点（固定小数点数・浮動小数点数）の表し方と正規化について
をご一読ください。
また、基数・進数・桁の重みについてより詳しく知りたい方は、
をご一読ください。基数についてより知ることができます！
浮動小数点数の誤差
コンピュータでは、表現できる数値は８ビット、３２ビット６４ビットなどとなっています。
表現できる数値は、決まっているビット内のみの範囲となるため、例えば１６ビットで表現するところ２進数の１７桁で表してほしい！と思っても範囲を超えるため、１７桁の２進数を表すことは１６ビットではできません。
また、割り算をして、割り切れない数値が解だとした場合、誤差が発生してしまいます。
例えば、１０進数の１０÷３で見てみましょう。
１０÷３＝３．３３３３３…このように永遠と３が続いてしまう状況にある数値を無限小数と言います。
表現できるビット数は限られているので、例えば８ビットで表現する場合、８ビット以下の数値は切り捨てされてしまうかもしれず、正確な数値とは言えません。
また、１０進数「０．１」を２進数に変換しようとした場合、
０．０００１１００１１００１１…と終わりが見えず、有効桁がきまっていると、どこかで切らなくてはいけません。
そのため、コンピュータではこのように終わりがない数値や有効桁を超えてしまう数値に対しては、正確な数値に一番近くなるような数値を出しているのです。
電卓で計算した場合も、同じように割り切れない場合や、表示できる桁を超えてしまう場合には、一番近い数値を表示しているのと同じです。
また、コンピュータでは、どんな時にどういった誤差が生じるかを５つに分類しています。
・桁あふれ誤差
・情報落ち
・打ち切り誤差
・丸め誤算
・桁落ち桁あふれ誤差（オーバーフロー・アンダーフロー）
桁あふれ誤差とは、演算結果の値が、コンピュータが表現できうる有効桁の範囲の最大値や最小値（上限や下限）を超えてしまうことにより生じる誤差を言います。
桁あふれ誤差で有効桁の範囲の最大値（上限）を超えることを「オーバーフロー」
桁あふれ誤差で有効桁の範囲の最小値（下限）を超えることを「アンダーフロー」と呼びます。
例えば４桁まで表示できる電卓があるとします。
この電卓で「９９９９」よりも演算結果が大きい場合の誤差が「桁あふれ誤差（オーバーフロー）」になります。
逆に「０．００…０１」のように小さすぎる（０に近い数）場合の誤差が「アンダーフロー」になります。
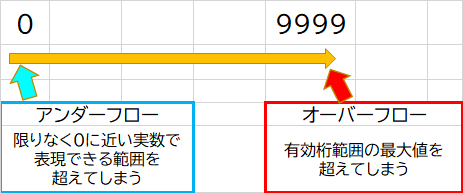
絶対値で大きすぎる場合発生するのがオーバーフローで、
絶対値で小さすぎる（０に近い数）場合発生するのがアンダーフローです。
また、固定小数点数で最小と最大を超えた場合（８ビットの場合）は
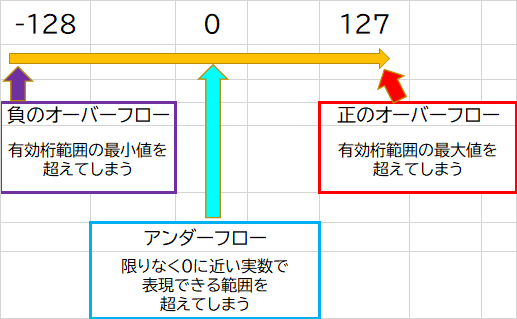
となります。
情報落ち
情報落ちとは、絶対値の大きな数値と絶対値のとても小さな数値との演算によって、絶対値のとても小さな数値が、計算結果に反映されないことにより生じる誤差を言います。
例えば４桁まで表示できる電卓があるとします。
１０００－０．００１
＝９９９．９９９上記の計算を４桁電卓で行った場合、
解の９９９．９９９は有効桁の範囲が４桁のため、
１０００－０．００１
＝１０００（０．９９９が無視されてしまう）となってしまうのです。
この小さな数値が結果に反映されないことを「情報落ち」と言います。
また、仮数部が４桁の１０進数で正規化をした場合を例に上げてみます。
（０．１２３４×１０²）＋（０．１２３４×１０⁻²）指数を揃えます。
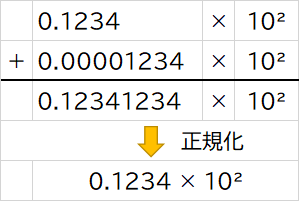
仮数部の有効桁の範囲は４桁のため、
０．００００１２３４は無視され、なかったことにされてしまいました。
浮動小数点数で、小さな数値が結果に反映されないことがあることが分かりました。この反映されない小さな数字が「情報落ち」です。
打切り誤差
打切り誤差とは、コンピュータでの計算処理を完了を待たず途中で打ち切ることにより生じる誤差のことです。
例えば、１０進数の１０÷３で見てみましょう。
１０÷３＝３．３３３３３…このように無限小数となってしまう数値に対し、永遠と計算をし続けることはできないので、途中で計算を打ち切らなくてはいけません。
本当は３．３３３３３３３…という結果なのに対し、計算を途中で打ち切り３．３３３という数値になった場合に実際の結果と打ち切った結果で誤差が生じてしまいます。
この誤差が「打切り誤差」です。
円周率も永遠に終わらない数値として有名です。
３．１４１５９２６５３５９…この場合も「３．１４」など途中で計算を打ち切っているので、正確な円周率との間に生じる誤差も「打切り誤算」となります。
丸め誤算
丸め誤算とは、有効桁数を超えてしまい、最小桁より小さい部分を四捨五入や切り上げ、切り捨てなどを行って表示することで生じる誤差のことです。
例えば、１０進数「０．１」を２進数に変換しようとした場合、
０．０００１１００１１００１１…と終わりが見えない無限小数となってしまうため、表現できる有効な桁が小数点以下８桁だとすると、
０．０００１１００１と、表現できる有効桁以降を切り捨てて表示します。
表現できる有効桁以降の値を四捨五入・切り上げ・切り捨てなどをして削った（丸めた）時、本当の数値と削った数値との間に生じる誤差が「丸め誤差」になります。
桁落ち
桁落ちとは、絶対値がほぼ等しい数値同士の引き算をした時に、有効桁数が大きく減ることによって生じる誤差のことです。
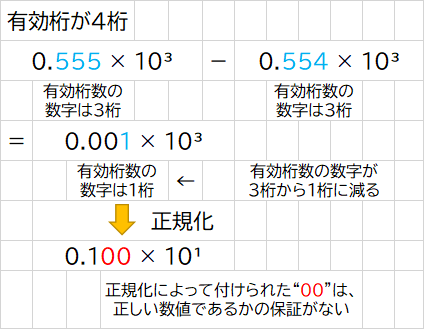
正規化をすることによって、有効桁数が増える物の自動で付けられた“００”は、本当に正しい数値なのか保証ができない＝信用できないのです。
まとめ
浮動小数点数の誤差について分かったでしょうか？
どう違うのかがこんがらがってしまいやすいですが、
1つずつ押さえていくことで、覚えやすくなるはずです。
正社員／フリーランスの方でこのようなお悩みありませんか？
- 自分に合う案件を定期的に紹介してもらいたい
- 週2、リモートワークなど自由な働き方をしてみたい
- 面倒な案件探し・契約周りは任せて仕事に集中したい
そのような方はぜひ、Workteriaサイトをご利用ください！
定期的にご本人に合う高額案件を紹介
リモートワークなど自由な働き方ができる案件多数
専属エージェントが契約や請求をトータルサポート
よく読まれている記事